All
동적 프로그래밍이란?
크기가 작은 문제(소문제)의 해를 테이블에 저장하고, 이를 이용해 점진적으로 더 큰 문제의 해를 찾아가는 상향식(Bottom-Up) 접근 방법
•
각 소문제는 원래 문제와 완전히 동일한 형태이며, 단지 입력 크기만 작아진 문제
•
“프로그래밍” 이라는 표현은 컴퓨터 프로그램과 무관하고, 해를 구축하는 데 테이블을 사용하는 계획법(planning)의 의미로 사용
•
주로 최솟값/최댓값을 구하는 최적화 문제에 사용
•
동적 프로그래밍이 적용 가능한 문제는 반드시 최적성의 원리(Principle of Optimality)를 만족해야 한다.
최적성의 원리
큰 문제의 최적해는 작은 문제들의 최적해로 구성된다
즉, 어떤 큰 문제의 최적해를 얻기 위해서는, 그 문제를 구성하는 작은 문제들 각각의 최적해를 반드시 먼저 구해야 한다는 의미
동적 프로그래밍 방법의 처리 과정
1.
주어진 문제가 최적성의 원리를 만족하는지 확인
2.
문제의 최적해를 제공하는 점화식(recursive formula)을 도출
3.
가장 작은 소문제부터 점화식을 이용해 해를 구하고 이를 테이블에 저장
4.
테이블의 소문제 해를 활용하여 상위 문제의 해를 차례로 구함
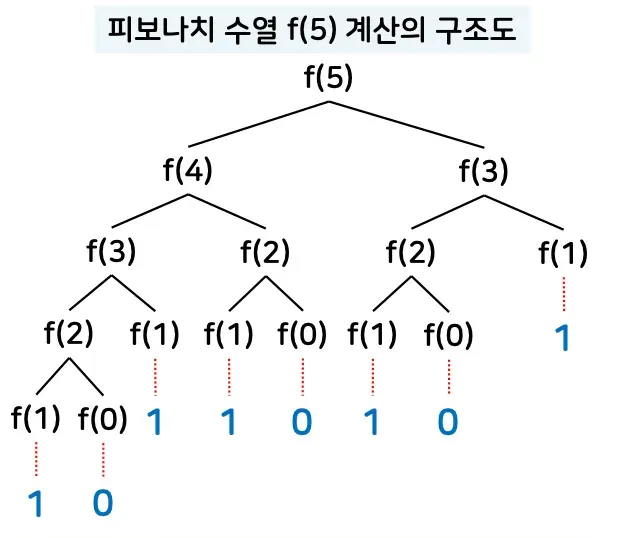
피보나치 수열
동적 프로그래밍의 개념을 쉽게 설명할 수 있는 대표적인 예제
반복문으로 구현
def fibo(n):
f = [0, 1] + [0]*(n-1)
for i in range(2, n+1):
f[i] = f[i-1] + f[i-2]
return f[n]
Python
복사
→ 시간복잡도
분할정복(재귀)으로 구현
def fibo(n):
if n <= 0:
return 0
if n == 1:
return 1
else:
return fibo(n-1) + fibo(n-2)
Python
복사
→ 시간복잡도
이 방법은 아래와 같이 동일한 계산을 여러 번 반복하기 때문에 매우 비효율적
DP 사용
def fibo(n):
f = [0, 1]
for i in range(2, n + 1):
f.append(f[i - 1] + f[i - 2])
return f[n]
Python
복사
→ 시간복잡도
계산한 값을 f 배열에 저장해두고, 다음 계산에 재사용하여 중복 계산을 피함
행렬의 연쇄적 곱셈
여러 개의 행렬을 곱할 때 어떤 순서로 곱하면 계산이 가장 적게 드는지를 찾는 문제
•
행렬 곱셈에서는 결합 법칙이 성립하기 때문에 괄호 위치(계산 순서)를 바꿔도 결과는 같지만
•
곱셈에 필요한 연산 수(계산량)는 순서에 따라 크게 달라질 수 있음
행렬 곱셈
두 행렬의 곱셈은 아래와 같은 규칙을 따름
•
•
계산량은
예시: 세개의 행렬을 곱할 때
•
아래 두 표현은 결과는 같지만 계산 순서에 따라 계산량이 달라짐
◦
(
◦
A: 10 x 100
B: 100 x 5
C: 5 x 50
1.
(A×B)×C 순서로 계산하면
•
A × B: 10 × 100 × 5 = 5,000
•
(A × B) × C: 10 × 5 × 50 = 2,500
•
총 계산량 = 7,500
2.
A×(B×C) 순서로 계산하면
•
B × C: 100 × 5 × 50 = 25,000
•
A × (B × C): 10 × 100 × 50 = 50,000
•
총 계산량 = 75,000
→ 계산량이 10배나 차이나므로 곱하는 순서가 중요함
예시와 같이 행렬이 3개일 때는 가능한 경우의 수가 2개뿐이라 직접 비교할 수 있지만, 행렬이 n개일 경우에는 가능한 괄호 묶음의 수가 기하급수적으로 증가
→ 효율적인 계산 순서를 찾는 방법이 바로 동적 프로그래밍인 것
연쇄 행렬 곱셈의 최적성 원리
n개의 행렬을 곱할 때의 최적의 곱셈 순서에는 그 안의 작은 부분 곱셈도 최적의 순서로 되어 있어야 한다
•
전체 곱셈 순서가 최적이려면 그 안에 있는 모든 작은 부분 곱셈 순서도 각각 최적인 상태여야 함
•
그래야 최적성의 원리를 만족하고 동적 프로그래밍 방법으로 해결 가능
예시
어떤 행렬 7개를 곱해야 한다고 했을때,
다음 괄호처럼 묶는 것이 가장 계산량이 적다고 한다면
M3, M4, M5를 곱하는 순서 또한 처럼 최적인 방식으로 이루어져 있어야 전체 순서가 최적이라고 할 수 있음
연쇄 행렬 곱셈 문제의 점화식
구현
def min_mat_mult(n, d):
C = [[0]*(n+1) for _ in range(n+1)]
for length in range(2, n+1):
for i in range(1, n-length+2):
j = i + length - 1
C[i][j] = float('inf')
for k in range(i, j):
cost = C[i][k] + C[k+1][j] + d[i-1]*d[k]*d[j]
if cost < C[i][j]:
C[i][j] = cost
return C[1][n]
Python
복사
성능 및 특징
•
시간복잡도:
◦
최소 계산량(C 테이블)을 구하는 데 필요한 시간
•
최적 곱셈 순서 복원 알고리즘
◦
계산과정에서 나눈 위치 k를 `p[i][j]`에 저장
◦
이를 재귀적으로 따라가며 괄호 위치를 복원
◦
n개의 행렬을 곱할 땐 n-2개의 괄호가 필요함
최장부분 공통 수열(Longest Common Subsequence LCS)
•
두 스트링의 공통된 부분 수열 중 가장 긴 수열을 찾는 알고리즘
•
여기서 부분 수열은 스트링에서 연속일 필요는 없지만 순서는 유지되어야함
•
예:
◦
X = SNOWY
◦
Y = SUNNY
→ SNY
LCS에서 최적성 원리
두 스트링 X와 Y의 LCS는 다음 세 가지 경우 중 하나
1.
X와 Y의 마지막 문자가 같다면, 그 문자를 포함한 앞 부분의 LCS + 마지막 문자
2.
X의 마지막 문자가 LCS에 포함되지 않는다면, X의 마지막 문자를 제외한 LCS
3.
Y의 마지막 문자가 LCS에 포함되지 않는다면, Y의 마지막 문자를 제외한 LCS
LCS의 점화식
구현
def LCS(X, Y):
m, n = len(X), len(Y)
L = [[0]*(n+1) for _ in range(m+1)]
for i in range(1, m+1):
for j in range(1, n+1):
if X[i-1] == Y[j-1]:
L[i][j] = L[i-1][j-1] + 1
else:
L[i][j] = max(L[i-1][j], L[i][j-1])
return L[m][n]
Python
복사
예시
- S U N N Y
-------------------
- | 0 0 0 0 0 0
S | 0 1 1 1 1 1
N | 0 1 1 2 2 2
O | 0 1 1 2 2 2
W | 0 1 1 2 2 2
Y | 0 1 1 2 2 3
Plain Text
복사
1.
(1,1) → X[0] = S, Y[0] = S
→ 같으니까 L[1][1] = L[0][0] + 1 = 1
2.
(2,3) → X[1] = N, Y[2] = N
→ 같으니까 L[2][3] = L[1][2] + 1 = 2
3.
(5,5) → X[4] = Y, Y[4] = Y
→ 같으니까 L[5][5] = L[4][4] + 1 = 3
나머지 칸은 전칸의 최대값으로 채움 (max(L[i-1][j], L[i][j-1]))
최종 결과는 L[5][5] = 3 → LCS 길이
성능 및 특징
•
시간 복잡도:
◦
모든 i, j 쌍에 대해 L[i][j]를 채워야 하므로 중첩된 이중 루프
•
테이블 LCS[][]로부터 LCS를 구하는 알고리즘(문자열 복원):
◦
테이블 오른쪽 아래에서 시작해 왼쪽 위로 이동하며 추적
◦
최악의 경우, 위 또는 왼쪽으로 한 칸씩만 움직이면 최대 n + m 번 움직이게 됨
→ 그래서 문자열 복원 알고리즘의 시간복잡도는 O(n + m)