All
트리의 개념
•
트리는 계층적(hierarchical) 관계를 표현하는 자료구조로, 노드와 간선으로 구성됨
•
root에서 시작해 여러 자식 노드로 뻗어나가며ㅡ 부모-자식 관계를 가짐
특징
•
루트(root) 노드는 단 하나뿐
•
각 노드는 0개 이상의 자식(child)을 가질 수 있음
•
루트를 제외한 모든 노드는 단 하나의 부모(parent)를 가짐
•
레벨(level): 루트로부터의 거리
예) 루트가 레벨 0이라면, 그 자식은 레벨 1, 손자 노드는 레벨 2 …
•
높이(height): 트리에서 가장 깊은 레벨의 수
추상자료형
생성 및 소멸 관련
1.
Tree Create() → 트리를 새로 생성하고, 루트 노드를 가리키는 포인터(참조값)를 반환
2.
Destroy(Tree) → 더 이상 사용하지 않는 트리의 모든 노드를 메모리에서 해제하고 시스템에 반환
3.
Tree Copy(Tree) → 기존 트리를 복사하여 동일한 구조의 새 트리를 만들고, 새 루트 노드의 포인터를 반환
노드 삽입·삭제·탐색
1.
Insert(n) → 트리에 노드 n을 삽입
2.
Delete(n) → 트리에서 노드 n을 삭제
3.
Search(x) → 트리 안에서 값이 x인 노드를 탐색해 찾으면 true, 없으면 false를 반환
탐색 및 속성 확인
1.
Traverse() → 트리를 순회하며 방문한 노드의 값을 순서대로 반환
2.
Root() → 트리의 루트 노드 값을 반환
3.
Parent(n) → 노드 n의 부모(또는 부모 포인터)를 반환 (n이 루트라면 오류 반환)
4.
Children(n) → 노드 n의 자식(들) 또는 그 포인터를 반환 (자식이 없으면 오류 반환)
노드의 상태 검사
1.
IsRoot(n) → 노드 n이 루트이면 true, 아니면 false
2.
IsInternal(n) → 노드 n이 내부 노드이면 true, 아니면 false
3.
IsLeaf(n) → 노드 n이 단말(leaf) 노드이면 true, 아니면 false
4.
IsEmpty() → 트리가 비어 있으면 true, 아니면 false
값 변경
1.
Replace(n, m) → 트리에서 노드 n을 노드 m으로 교체
이진트리 Binary Tree
•
모든 노드의 차수가 2 이하인 트리
•
특징
◦
자식 노드는 왼쪽과 오른쪽으로 구분
◦
트리의 각 노드에서 두 갈래로 나뉘는 구조
◦
공집합도 유효한 이진 트리로 간주
이진 트리의 주요 용어
•
루트(root): 트리의 시작 노드
•
왼쪽 서브트리(left subtree), 오른쪽 서브트리(right subtree)
•
단말 노드(leaf node): 자식이 없는 노드
•
내부 노드(internal node): 자식이 하나 이상인 노드
•
트리의 높이(height): 가장 긴 경로의 간선 수
이진 트리 종류
•
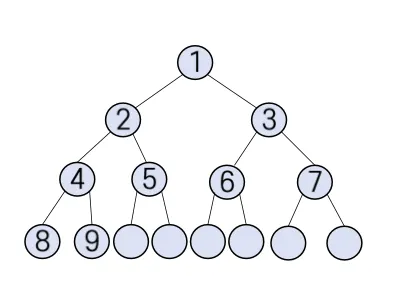
포화 이진 트리 (perfect binary tree): 모든 내부 노드가 두 개의 자식 노드를 가지고, 모든 leaf 노드는 같은 레벨에 있는 이진 트리 (트리 전체가 꽉찬 것)
•
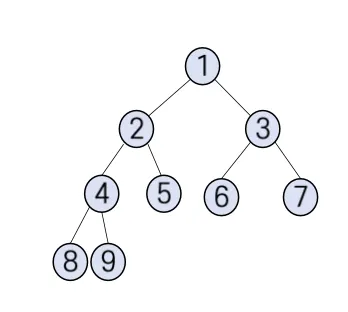
완전 이진 트리 (complete binary tree): 트리의 마지막 레벨을 제외한 모든 레벨이 완전히 채워져 있고 마지막 레벨의 노드들은 왼쪽부터 차례대로 채워진 이진 트리
이진 트리의 구현방법
•
이진 트리는 배열이나 포인터두 가지 방식으로 구현할 수 있음
•
각 방식은 메모리 구조나 접근 효율에 차이가 있음
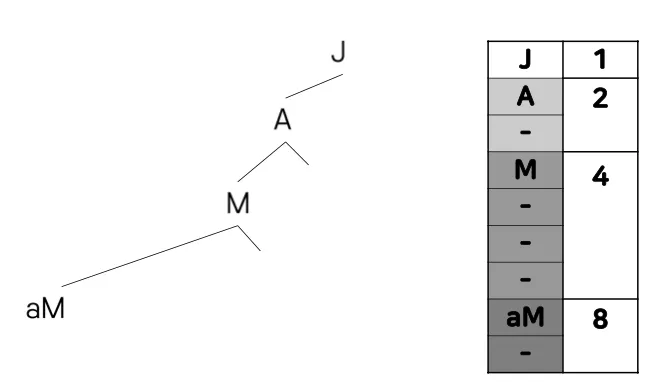
배열을 이용한 구현
•
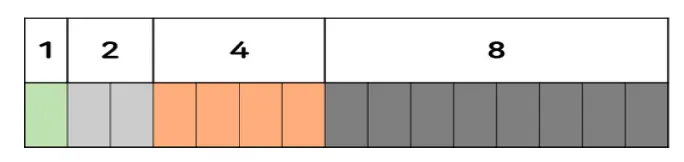
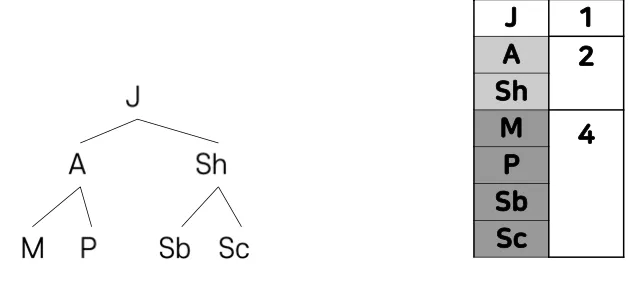
트리의 노드를 배열의 인덱스로 표현하는 방식
•
인덱스를 이용해 부모-자식 관계를 계산할 수 있음
◦
루트 노드의 인덱스: 1
◦
왼쪽 자식 인덱스 = 2 * i
◦
오른쪽 자식 인덱스 = 2 * i + 1
◦
부모 인덱스 = i // 2
장점
•
트리가 완전/포화 이진 트리 일 경우 배열내 빈공간이 거의 없어 효율적
•
인덱스 계산만으로 부모나 자식 노드를 빠르게 찾을 수 있음
단점
•
트리가 한쪽으로 치우쳐질수록(skewed) 인덱스가 커지며 낭비되는 공간 급격히 증가
•
깊이가 깊을수록 배열 크기가 2의 거듭제곱 수준으로 커짐
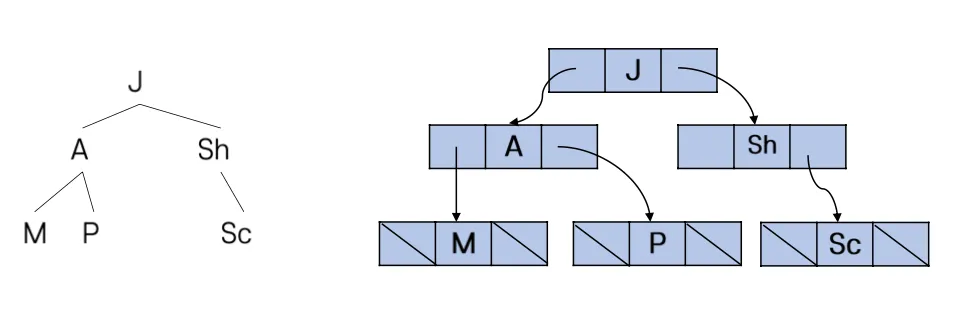
포인터를 이용한 이진트리의 구현
•
각 노드가 자기 자신을 구조체(struct)로 가지며 왼쪽 자식과 오른쪽 자식을 포인터로 연결하는 방식
•
노드의 위치는 메모리 상에서 흩어져 있지만 포인터를 통해 논리적 연결 구조를 유지
구조체 정의 예시
typedef struct node {
struct node *left; // 왼쪽 자식 노드의 주소
char data; // 노드 데이터
struct node *right; // 오른쪽 자식 노드의 주소
} node;
C
복사
•
한 노드는 데이터 1개 + 왼쪽/오른쪽 포인터 2개로 구성됨
[ *left | data | *right ]
장점
•
트리 모양이 불균형하더라도 메모리 낭비가 없음
•
트리의 확장, 삭제, 삽입이 용이 (포인터 연결만 바꾸면 됨)
단점
•
부모-자식 탐색 시 포인터를 따라가야 하므로 접근 속도가 느림
•
포인터를 저장할 공간(메모리) 필요
이진 트리 순회
트리의 모든 노드를 일정한 순서로 방문하는 방법으로 대표적으로 3가지 방식 있음
트리 구조(예시용)
1
/ \
2 3
/ \ \
4 5 6
/
7
C
복사
전위 순회 Preorder Traversal, PLR
•
루트(Parent) → 왼쪽(Left) → 오른쪽(Right)
•
루트를 먼저 처리
방문 순서
•
1 → 2 → 4 → 5 → 3 → 6 → 7
void preorder(node* root) {
if (root != NULL) {
printf("%c ", root->data); // 루트 방문
preorder(root->left); // 왼쪽 서브트리 방문
preorder(root->right); // 오른쪽 서브트리 방문
}
}
C
복사
중위 순회 Inorder Traversal, LPR
•
왼쪽(Left) → 루트(Parent) → 오른쪽(Right)
•
이진 탐색 트리(BST)에서는 오름차순 정렬된 순서로 출력된다는 특징이 있다
방문 순서
•
4 → 2 → 5 → 1 → 7 → 6 → 3
void inorder(node* root) {
if (root != NULL) {
inorder(root->left); // 왼쪽 서브트리 방문
printf("%c ", root->data); // 루트 방문
inorder(root->right); // 오른쪽 서브트리 방문
}
}
C
복사
후위 순외 Postorder Traversal, LRP
•
왼쪽(Left) → 오른쪽(Right) → 루트(Parent)
•
주로 트리의 메모리 해제 같은 경우 많이 사용
방문 순서
•
4 → 5 → 2 → 7 → 6 → 3 → 1
void postorder(node* root) {
if (root != NULL) {
postorder(root->left); // 왼쪽 서브트리 방문
postorder(root->right); // 오른쪽 서브트리 방문
printf("%c ", root->data); // 루트 방문
}
}
C
복사
이진 트리 연산
이진 트리의 생성
•
일반적으로 연결 리스트 연산을 이용해 트리를 생성
•
첫 번째 노드가 만들어지면 루트 노드가 되고,
•
새로운 노드를 추가할 때는 연결 리스트의 삽입 연산을 이용
즉, 트리의 노드 연결도 결국 포인터로 서로 연결된 구조체를 이용해서 구성됨.
이진 트리 노드 삽입
•
새로운 노드를 추가할 때, 비어있는(=NULL) 자리에 노드를 연결한다
•
삽입할 위치(here)가 비어 있으면 그 자리에 새로운 노드(it)를 연결
node *insert(node *here, node *it) {
if (here == NULL) {
here = it;
return NULL;
} else {
node *victim;
victim = here;
*here = *it;
return victim;
}
}
C
복사
•
here == NULL이면 → 그 자리가 비어 있으므로 바로 it을 삽입
•
이미 노드가 있으면 → 기존 노드(victim)을 저장하고 새 노드로 덮어씀
•
이때 포인터 조작으로 연결을 갱신
이진 트리의 노드 삭제
•
삭제 대상 노드를 찾아서 해당 포인터를 NULL로 바꾸고, 메모리 해제(free)
•
만약 삭제하려는 노드가 부모의 왼쪽 자식인지 오른쪽 자식인지에 따라 구분
•
삭제하려는 노드가 자식 노드를 가지고 있으면, 그 자식 노드 처리도 함께 필요
node *delete(node *root, node *it, char direction) {
node *parent = searchParent(root, it);
if (parent == NULL) {
printf("삭제 불가!\n");
return NULL;
} else {
if (direction == 'l') {
parent->left = NULL;
free(parent->left);
return it;
} else if (direction == 'r') {
parent->right = NULL;
free(parent->right);
return it;
} else
return NULL;
}
}
C
복사
•
searchParent(root, it) → 삭제하려는 노드의 부모를 찾음
•
direction은 'l' 또는 'r'로 자식 방향을 구분
•
해당 자식 포인터를 NULL로 바꾸고, free()로 메모리 해제
이진 트리의 노드 개수 세기 (Count Nodes)
•
루트를 기준으로 왼쪽 서브트리 + 오른쪽 서브트리 + 자기 자신(1)
•
재귀적으로 모든 노드를 순회하면서 카운트
int get_nodeNum(node *root) {
int num = 0;
if (root == NULL) {
return 0;
} else {
num = 1; // 자기 자신
num += get_nodeNum(root->left) + get_nodeNum(root->right);
return num;
}
}
C
복사
•
재귀 호출로 모든 노드를 한 번씩 방문
•
비어있지 않으면 1을 더하고, 왼쪽과 오른쪽 서브트리의 노드 수도 더함
•
최종 결과 → 트리 전체 노드의 개수
이진 트리의 리프 노드 개수 세기
•
리프(leaf) 노드는 왼쪽과 오른쪽 자식이 모두 NULL인 노드
•
각 노드를 검사하며 리프면 1을 반환
int get_leafNum(node *root) {
int result = 0;
if (root == NULL) {
return 0;
} else if (root->left == NULL && root->right == NULL) {
return 1; // 리프 노드
}
result += get_leafNum(root->left) + get_leafNum(root->right);
return result;
}
C
복사
•
루트가 NULL이면 0
•
둘 다 NULL이면 리프이므로 1
•
왼쪽·오른쪽 서브트리를 재귀적으로 탐색하여 리프 개수를 합산